Basic numbers

In the previous version of this blog I focused specifically on the concepts of anticryptography. I had written a post about the universality around numbers. While I was thinking of reposting the original it became obvious that the subject was important to me and needed to be rewritten.

How to talk to aliens

While anticryptography can mean as little as a self describing format, sometimes even that format may not be obvious. We don’t know what concepts are uniform and shared between any group of users of the data. As an American I may default to thinking 7-bit ASCII and English words are obvious, but the majority of the world realizes I’m being stupid in making that assumption (yet for so many years they just went along with it and learned English. Enablers!).

We could be trying to project the information across spatial, temporal or cultural chasms. What I write here may make no sense to someone in China or the year 1600 (or 3600). The opposite may be true, although we have a historic record that let’s us try and understand something from 1600. That gets harder the further back we go despite all of the attempts of historians and archaeologist.

We can’t predict what those gaps in thought will be so there is a thought experiment that can be useful. Instead of trying to explain it to a different human, what if it was an alien lifeform? They share no common frame of reference with us from biology, history or culture. They really only share the universal laws of the cosmos with us. We represent those laws with math and it is likely any advanced civilization is also using math for similar reasons. If we can express concepts with math things might be workable.

There is no way of writing a formula that will be universal (we have had more than one notation in the last few centuries ourselves), so we need to work from base concepts. Any civilization with advanced technology has most likely worked with discrete items. This means the concept of counting and integers are probably easily shared. Basically we should start with numbers.

Numbers everywhere

First off we need to just start with plain old integers. I made a crude first attempt in the cover photo. To most observers it will look like counting items out to represent the numbers 1-4, but even there we need to be careful. By using things I have laying around my desk I found rubber feet for numbers 1 and 2 and used screws for the numbers 3 and 4. An alien may perceive them as counting different things or the threads as a parameter. Who knows, the graph of the engineering pad could be picked up as a concept more important than the items. It will be important to use a uniform, plain item in a plain environment.

Using a circle is a good choice. The rubber feet would be a good reference for physical items. They have very few features and can be made uniform enough to prevent confusion. By laying them out in isolated arrangements we could convey the meaning of our Arabic numerals 0-9.

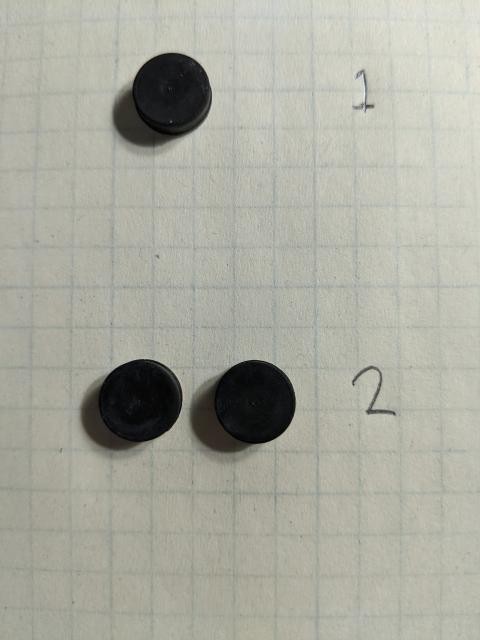
Having multiple examples where the items are arranged vertically diagonally, in a matrix and a random cloud will help the observer understand that the count is what the written symbol represents. With a couple pages of this we can be assured the observer probably understands our single digit numbers and is bored enough to move on.

The observer probably has an idea we are using base 10 given the number of symbols, but it isn’t a slam dunk. Showing them how we represent numbers larger than 9 is a leap and borders on addition, so much so I would introduce addition before multiple digits.

Operations

With addition we can start building up higher order concepts. We should probably use the ‘=’ sign in the previous mappings to introduce it’s meaning and make it’s use obvious here. With the 2 operator symbols, the single digits and our items we can start enumerating through many, is not all, of the additions that produce single digit results. Here are a few examples.

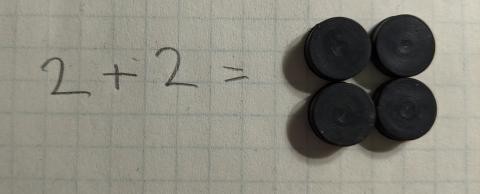
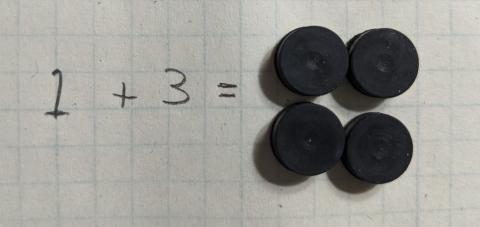
So hopefully we have a rhythm going with our alien reader and they start understanding the concepts of + and = and single digit numbers. From there we can figure out how to represent double and then triple digit numbers to show how our numbering system works with countable integers through any tangible number. The number of examples will not need to be as large if we did our job correctly before, but will need to cover corner cases (how do we roll over from 9 to 10 and 99 to 100) fairly fully.

Negative

Subtraction and negative numbers go hand in hand in the next step even if we don’t teach it that way to our own kids (we should though). Hopefully the previous examples up to that point are sufficient that introducing the symbol and some examples would be sufficient. Remember we aren’t trying to teach arithmetic in this thought experiment, just map our symbols to someone else’s version.

Higher order concepts

With integers, addition, negative and subtraction we can build on those to represent multiplication and fractions. I would skip division as it really isn’t a concept that is needed so long as fractions are understood. It would just get in the way.

From there it is possible to start build up and map all of the arithmetic concepts (square roots and exponents for example). We can bring other items back in and start using them as a different type and start mapping algebra. From there calculus becomes possible following the same methods. With calculus things get really rich.

This all may require a large tome of examples to make sure the concepts are not vague or misunderstood. While an alien scholar may spend time learning them, there needs to be short cuts to make sure attention spans don’t get in the way.

Software to the rescue

It is more likely that we could make a programming language that would map the concepts faster and easier. First off, Base 10 is really a poor choice for anyone that isn’t human. Binary is so simple the concepts are easier to convey. Base 3 is more optimal for representing things (the optimal base is e but that is another story), but binary makes things easier.

Second, the only operation we need to convey to our alien is that of AND and NOT. Yep, from those 2 we can make any other operation through application of De Morgan’s law. We aren’t far from a basic programming language now. Think I’m pulling your leg? Turing machines weren’t much more and that is the perfect target.

Turing computable

The concepts behind Turing completeness and computability are fascinating, but I’ll sum it up quickly here.

Anything that can be computed by a Turing complete language can be done by a Turing machine given enough time and memory. The reverse holds true also.

If you can write it in C I can also write it and run it in Python, Forth, Lisp or any other language (obviously there are machine dependent features that don’t map, but we are only concerned with the math), given enough memory and time. What does this mean for the alien diplomacy thought experiment? We only need a simple programming language, really simple. Single operator (NAND since we can get a NOT and AND out of it with some simple combinations) and a way to apply it to numbers and references to numbers in memory.

Don’t believe me yet again? Well, it’s rough programming only using NAND and a few addressing modes, but you can see something almost as simple in the living flesh with …

Brainfuck

That’s not a typo and the blog hasn’t been hacked to put an obscenity up. That is the name of a real programming language. It uses 8 symbols, total. There are symbols for incrementing, decrementing, input, output and comparison for zero value. You can write whole programs in it and in theory given enough time and memory it can do anything any other programming language can. Here are some examples.

++++++++[>++++[>++>+++>+++>+<<<<-]>+>+>->>+[<]<-]>>.>---.+++++++..+++.>>.<-.<.+++.------.--------.>>+.>++.

That prints “Hello World!”

,[.,]

Outputs what you input. That’s actually amazingly simple.

Once the concepts are understood the reader can pencil through simple programs and get to higher order answers. They can also implement their own version and run advanced programs to see the output and gain knowledge. BF interpreters can be as short as 100 bytes long and are rarely much more than 2-3 times that without optimizers. Once our alien counterpart understands the language we can send large complex concepts and have identical output. That let’s up skip over a lot of “accounting” work we alluded to earlier.

We don’t even need to write the larger programs in BF as it can be a compiler target. Write code in C for instance and have a compiler output BF. This frees the writer up to do more complex thinking. On the other side it is likely to happen also.

Wrapping it up

I think if we stop thinking of ourselves as the reader this becomes simple. We have to represent binary and some simple Boolean logic to them. After that we represent a Turing machine like programming language that can be implemented easily. From there we can use the concepts of programming to cover space quicker and convey math through a discreet set of symbols that execute as code.

In previous posts I’ve talked about programming languages to preserver ideas in. Remember this is a thought experiment for conveying ideas to aliens. While I will continue to expand on it, it isn’t how I would preserve information in general. For the thought experiment we could build a ramp to a more ideal preservation language and format, but once basic numbers and operations are in place we will want to move faster.